Conjuntos de Números Enteros y sus Propiedades

·         Conjunto de números enteros (z) y sus propiedades:

     Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor.

Por ejemplo, la necesidad de representar el dinero adeudado, temperatura bajo cero, profundidades con respecto al nivel del mar, etc.

     Las anteriores situaciones nos obligan a ampliar el concepto de números naturales, introduciendo un nuevo conjunto numérico llamado números enteros.

El conjunto de los números enteros está formado por:

Z = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}

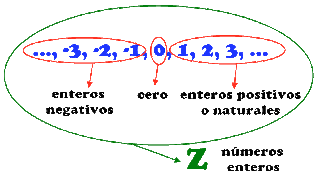
     Es decir, los naturales, sus opuestos (negativos) y el cero. Se dividen en tres partes: enteros positivos o números naturales, enteros negativos y cero.

Z=Z- U {0} U Z+

     Dado que los enteros contienen los enteros positivos, se considera a los números naturales son un subconjunto de los enteros.

N C Z

Criterios para ordenar los números enteros

1.      Todo número negativo es menor que cero.

 −7 < 0

2.      Todo número positivo es mayor que cero.

 7 > 0

3.      De dos enteros negativos es mayor el que tiene menor valor absoluto.

−7 >− 10 |−7| < |−10|

4.      De los enteros positivos, es mayor el que tiene mayor valor absoluto.

 10 > 7 |10| > |7|

Suma de números enteros

1.      Si los sumando son del mismo signo, se suman los valores absolutos y al resultado se le pone el signo común.

3 + 5 = 8 (−3) + (−5) = − 8

2.      Si los sumando son de distinto signo, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le pone el signo del número de mayor valor absoluto.

 − 3 + 5 = 2 3 + (−5) = − 2

Propiedades:

1. a 0 = 1

 2. a 1 = a

3. Producto de potencias con la misma base : Es otra potencia con la misma base y cuyo exponente es la suma de los exponentes.

a m · a n = a m+n

 (−2) 5 ·(−2) 2 = (−2) 5+2 = (−2) 7 = −128

4.División de potencias con la misma base : Es otra potencia con la misma base y cuyo exponente es la diferencia de los exponentes.

 a m : a n = a m – n

(−2) 5 : (−2) 2 = (−2) 5 - 2 = (−2) 3 = −8

1.      Potencia de una potencia : Es otra potencia con l a misma base y cuyo exponente es el producto de los exponentes.

(a m ) n = a m · n

[(−2) 3 ] 2 = (−2) 6 = 64

2.      Producto de potencias con el mismo exponente : Es otra potencia con el mismo exponente y cuya base es el producto de las bases

a n · b n = (a · b) n

 (−2) 3 · (3) 3 = (−6) 3 = −216 8

3.      Cociente de potencias con el mismo exponente : Es otra potencia con el mismo exponente y cuya base es el cociente de las bases.

 a n : b n = (a : b) n

(−6) 3 : 3 3 = (−2) 3 = −8

Propiedades de la multiplicación de números enteros

1.      Interna: El resultado de multiplicar dos números enteros es otro número entero.

 a · b E Z

2 · (−5) E Z

2.      Asociativa: El modo de agrupar los factores no varía el resultado. Si a, b y c son números enteros cualesquiera, se cumple que:

(a · b) · c = a · (b · c)

 (2 · 3) · (−5) = 2· [(3 · (−5)]

6 · (−5) = 2 · (−15)

-30 = -30

3. Conmutativa: El orden de los factores no varía el producto.

 a · b = b · a

2 · (−5) = (−5) · 2

-10 = -10

4. Elemento neutro: El 1 es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.

 a ·1 = a

 (−5)· 1 = (−5)

5. Distributiva: El producto de un número por una suma es igual a la suma de los productos de dicho número por cada uno de los sumandos.

 a · (b + c) = a · b + a · c

 (−2)· (3 + 5) = (−2) · 3 + (−2) · 5

 (−2)· 8 =- 6 - 10

-16 = -16

Propiedades de la suma de números enteros

1.      Interna: El resultado de sumar dos números enteros es otro número entero.

 a + b E Z

 3 + (−5) E Z

2.      Asociativa: El modo de agrupar los sumandos no varía el resultado.

 (a + b) + c = a + (b + c) ·

(2 + 3) + (− 5) = 2 + [3 + (− 5)]

5 − 5 = 2 + (− 2)

0        = 0

3.      Conmutativa: El orden de los sumando no varía la suma.

a + b = b + a

1        + (− 5) = (− 5) + 2

 − 3 = − 3

4.      Elemento neutro: El 0 es el elemento neutro de la suma porque todo número sumado con él da el mismo número.

 a + 0 = a

 (−5) + 0 = − 5

5.      Elemento opuesto: Dos números son opuestos si al sumarlos obtenemos como resultado el cero.

 a + (-a) = 0

 5 + (−5) = 0

 El opuesto del opuesto de un número es igual al mismo número.

−(−5) = 5.

Relación Con la vida cotidiana:

     Para mí este tema está relacionado con la vida cotidiana porque siempre nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor.